筆記：RSA 簽章驗證

RSA 是廣為使用的非對稱加密演算法，原本我以為已經很熟悉它了，想不到最近試圖用 Python 實作簽章驗證的時候，才發現有很多小細節是以前沒注意到的地方。

非對稱加密演算法

先複習一下大家熟到不能再熟的觀念。

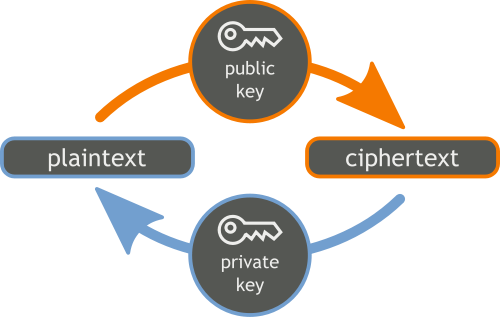
在非對稱加密演算法中，會有兩把鑰匙。使用其中一把鑰匙加密過的資訊，必需用另一把鑰匙才能解開。一般的使用情況是：

  1. 發送者使用公鑰加密訊息，接收者使用私鑰解開密文。
  2. 發送者使用私鑰簽署訊息，接收者使用公鑰驗證簽章。

非對稱加密演算法有很多種，像什麼 ElGamal 或橢圓曲線加密法之類的，其中最常用的是 RSA。

RSA 數學原理

一組 RSA 鑰匙對 (key pair) 包含了三個數字：$(N, e, d)$，其中：

  • $N$ 為兩個隨機產生質數 $(p, q)$ 的乘積。
  • $(e, d)$ 是由 $(p, q)$ 所計算出來，且對任意自然數 $n$ 都滿足以下條件：
    $ n^{ed} \equiv n \mod N $
  • 計算完 $(e, d)$ 後隨即丟棄 $(p, q)$。私鑰保留 $(N, e, d)$，公鑰則以 $(N, e)$ 的形式散布出去。

公鑰加密過程是把明文視為一個很大的數字 $n$，計算 $n^e$ 除以 $N$ 所得到的餘數：

$ c = n^e \mod N $

解密過程只是把上一步再作一次，但把 $e$ 代換成私鑰中的 $d$ 而已：

$ n = c^d \mod N $

實務上，因為加密和解密都是直接求餘數，因此必須限制 $n < N$，否則會導致解密出來的結果根本不是原來的 $n$。大於 $N$ 的訊息必需先切割成小區塊再個別加密。

簽章與驗證（錯誤示範）

簽章的原理很簡單：

  1. 發送者使用 MD5 或 SHA 之類的雜湊函數計算欲傳輸的訊息摘要 (digest)。
  2. 使用私鑰加密訊息摘要，並且和原本訊息一起傳送給接收者。
  3. 接收者使用公鑰解開摘要密文，並且用事先約定好的雜湊函數計算訊息摘要是否吻合。

若使用 openssl 來產生簽章，指令大概會像這樣：

1
2
3
$ openssl sha -binary data.txt \
| openssl rsautl -sign -inkey private_key.pem \
| base64

第一行產生 SHA1 digest，第二行使用私鑰簽章，最後使用 base64 編碼輸出。然而這是錯誤的做法，產生的簽章會被其它軟體視為假簽章。

PKCS#1 v1.5 加密標準

關鍵點在於填充位元 (padding bytes)。為了安全考量，使用 RSA 對訊息加密或簽章時，必需先對訊息補上特定的填充位元 (padding bytes)，才能進行加密。否則一些特殊的明文字串像是 0x00 或 0x01 加密後的結果和原來的明文一模一樣，就完全沒有加密效果了。

$ 0^e \mod N = 0 $
$ 1^e \mod N = 1 $
不管使用哪一支公鑰，0 和 1 都沒辦法加密

在大多數的應用場合中，都是遵循 PKCS#1 的規範來加入填充位元。在這套標準中，不同的雜湊函式要使用不同的填充位元，然而在前面的錯誤示範中，第二個 openssl 指令並不知道 pipe 進來的資料使用怎樣的雜湊函式，只好產生錯誤的填充位元。

正確的指令應該是這樣：

1
$ openssl sha -sign private_key.pem data.txt | base64

亦即在計算雜湊後馬上使用指定的私鑰簽章，讓 openssl 可以根據雜湊函數產生正確的填充位元。

使用 Python 實作

Python 有個 PyCrypto 函式庫，提供了各式加密演算法需要的功能，當然也包含了 PKCS#1。以下是簡單的實作：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from base64 import b64encode, b64decode
from Crypto.PublicKey import RSA
from Crypto.Hash import SHA
from Crypto.Signature import PKCS1_v1_5
def generate_rsa_sha1_signature(data, private_key):
    hash_obj = SHA.new(data)
    key = RSA.importKey(private_key)
    signer = PKCS1_v1_5.new(key)
    signature = signer.sign(hash_obj)
    return b64encode(signature)
def verify_rsa_sha1_signature(data, public_key, signature):
    hash_obj = SHA.new(data)
    key = RSA.importKey(public_key)
    signature = b64decode(signature)
    verifier = PKCS1_v1_5.new(key)
    return verifier.verify(hash_obj, signature)
分享到 評論